|
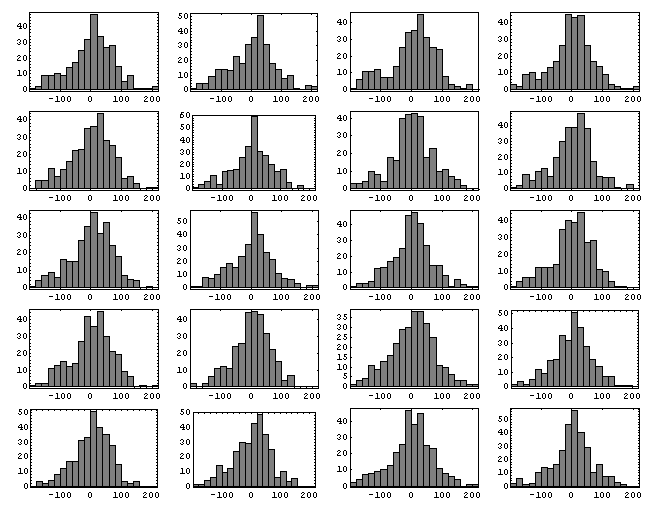
Error histograms and deviations for each beat
The following array of plots display histograms of beat-tapping
errors as compared to their manually corrected times. The errors are
referenced to the average of 20 reverse conducting of the performance
(an analysis of individual trials is given further below).
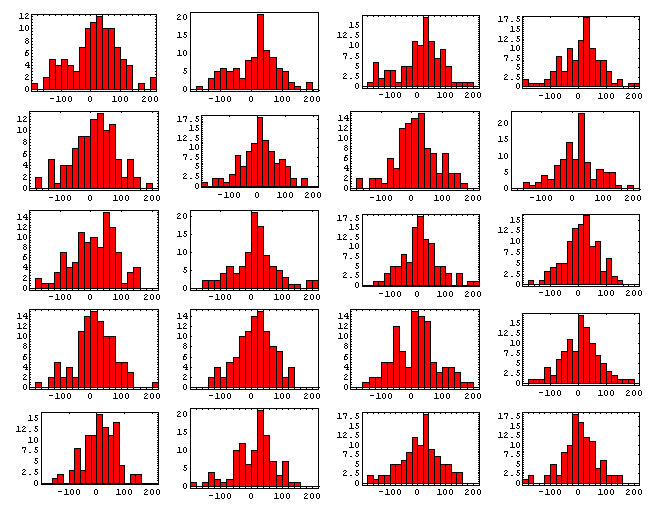
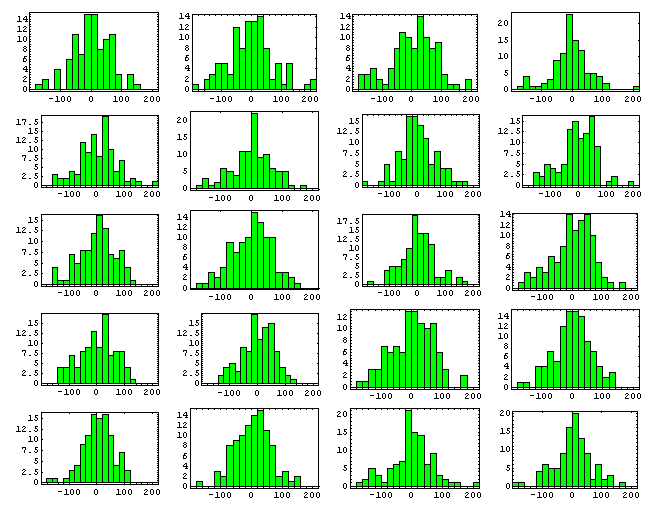
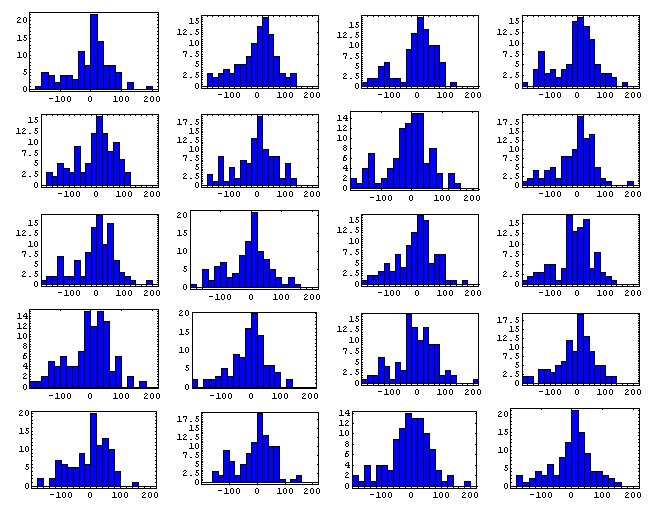
The first column of plots (in gray) display the tapping errors for
all beats in a performance. The following three columns of plots
separate beat errors according to metric position
(red=1, green=2 and blue=3).
The last row in the array of plots displays the histograms for
all four performances.
Beneath each plot is two numbers:
- The average displacement error (mean deviation) of taps from their manually corrected
positions.
- The standard deviation of the distribution of taps around their
manually corrected positions.
Performer
Mazurka |
| All Beats |
Beat 1 |
Beat 2 |
Beat 3 |
|
Chiu 1999
Op.7 No.2 | 
| md=46.5; sd=62.3 |
md=56.0; sd=72.2 |
md=36.1; sd=49.4 |
md=47.3; sd=63.4 |
|
Friedman 1930
Op.7 No.2 | 
| md=49.4; sd=69.3 |
md=64.6; sd=88.9 |
md=37.9; sd=50.2 |
md=45.7; sd=59.8 |
|
Friedman 1930
Op.7 No.3 | 
| md=41.3; sd=58.3 |
md=34.3; sd=44.0 |
md=49.0; sd=66.3 |
md=40.5; sd=60.9 |
|
Rosen 1989
Op.7 No.3 | 
| md=47.9; sd=64.5 |
md=47.8; sd=60.8 |
md=46.0; sd=60.3 |
md=50.0; sd=70.6 |
|
| All | 
| md=46.3; sd=63.6 |
md=50.9; sd=68.7 |
md=42.0; sd=56.6 |
md=45.9; sd=64.1 |
|
Note that mazurka Op. 7, No. 2 in A minor is in a slower tempo than
mazurka Op. 7, No. 3 in F minor. Also, the Friedman performance of Op. 7,
No. 3 was the first manually corrected performance, and it is also a difficult
recording to manually correct.
On the average over all beats in the four performances, tapping the
first beat is the hardest, with a median deviation of 50.9 milliseconds.
The easiest beat to tap was beat 2 which has a median deviation of
42.0 milliseconds. The 11.1 millisecond difference between the
average accuracies of beats one and two is small, but
probably significant.
In terms of individual performances, the most accurately placed
metric beats were: 2, 2, 1, 2. The least accurate metric beats
were: 1, 1, 2, 3.
Error characteristics of individual tapping trials
The error displacement of taps from the true beat given in the graphs
above are derived from the average of tapping twenty separate times to
the same performance, in this case Charles Rosen's 1989 performance of
Mazurka Op. 7, No. 3 in F minor. In this section, the individual tapping
trials are compared to the manually corrected beat times. The meaning of
the color of each plot is the same as in the previous section: gray=all
beats, red=beat 1, green=beat 2, and blue=beat 3.
Here is a list of the "best beat" for the metric position with the lowest
mean deviation in each of the 20 trials: 3, 3, 3, 2, 2, 2, 2, 1, 2, 1, 2,
3, 1, 3, 3, 2, 2, 2, 2, 2. The "worst beat" for each trial is:
1, 1, 2, 1, 1+3, 3, 1, 2, 1, 2, 3, 2, 2, 2, 2, 1, 1, 3, 1, 1.
The mean deviation and standard deviation for the displacement error
for each trial compared to the manually corrected timings can be found
in the Mathematica notebook used to do the analysis calculations.
Average duration of beats in metric cycle
In general, the durations of beats in the metric cycle of
a mazurka are not equal. This section measures the average
duration as a fraction of the metric cycle for each beat.
The beat in each measure was converted to a fraction of the measure.
If all three beats are equivalent in duration, then each would
take 33.3% of the full duration of the measure. Note that changes in
global tempo during a measure will confuse these measurements.
Performer
Mazurka |
| All Beats |
Beat 1 |
Beat 2 |
Beat 3 |
|
Chiu 1999
Op.7 No.2 | 
| 33% ± 5.1% |
35% ± 5.7% |
31% ± 3.3% |
34% ± 5.3% |
|
Friedman 1930
Op.7 No.2 | 
| 33% ± 6.1% |
31% ± 5.7% |
33% ± 5.2% |
36% ± 6.3% |
|
Friedman 1930
Op.7 No.3 | 
| 33% ± 6.7% |
32% ± 7.0% |
35% ± 5.9% |
33% ± 6.9% |
|
Rosen 1989
Op.7 No.3 | 
| 33% ± 6.2% |
32% ± 7.0% |
34% ± 5.1% |
34% ± 6.2% |
|
| All | 
| 33.3% ± 6.0% |
32.7% ± 6.5% |
33.2% ± 5.1% |
34.1% ± 6.3% |
|
Compare the manually corrected data (above) with data derived
from the average tapped durations of the beats (below). The main
noticeable difference is that the standard deviations are smaller (the
peaks are narrower), and also beats one and three do not show a side peak
in the 40% range).
Performer
Mazurka |
| All Beats |
Beat 1 |
Beat 2 |
Beat 3 |
|
Chiu 1999
Op.7 No.2 | 
| 33% ± 5.1% |
35% ± 5.9% |
31% ± 3.2% |
34% ± 5.1% |
|
Friedman 1930
Op.7 No.2 | 
| 33% ± 4.8% |
34% ± 4.1% |
32% ± 4.4% |
34% ± 5.5% |
|
Friedman 1930
Op.7 No.3 | 
| 33% ± 4.0% |
32% ± 3.6% |
33% ± 2.6% |
35% ± 5.0% |
|
Rosen 1989
Op.7 No.3 | 
| 33% ± 5.5% |
31% ± 5.7% |
33% ± 4.1% |
35% ± 5.8% |
|
| All | 
| 33.3% ± 4.9% |
32.9% ± 5.1% |
32.5% ± 3.7% |
34.5% ± 5.3% |
|
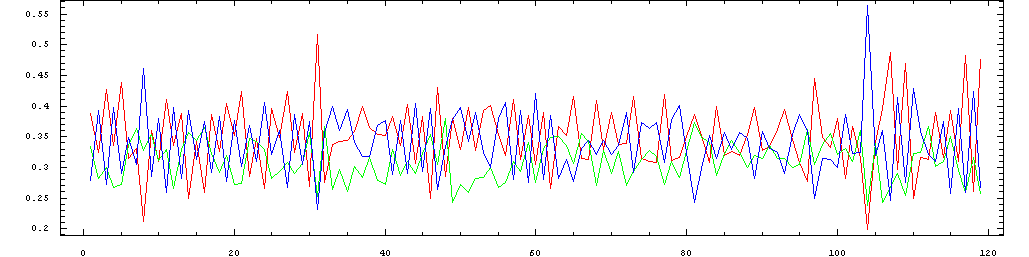
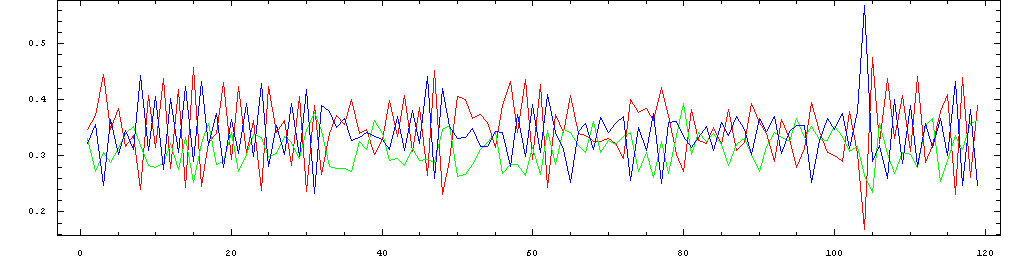
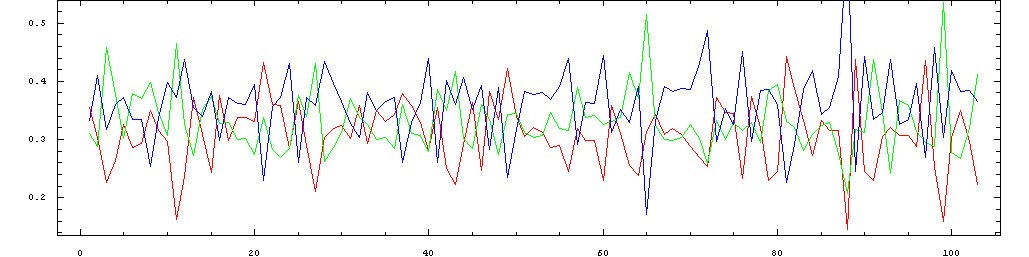
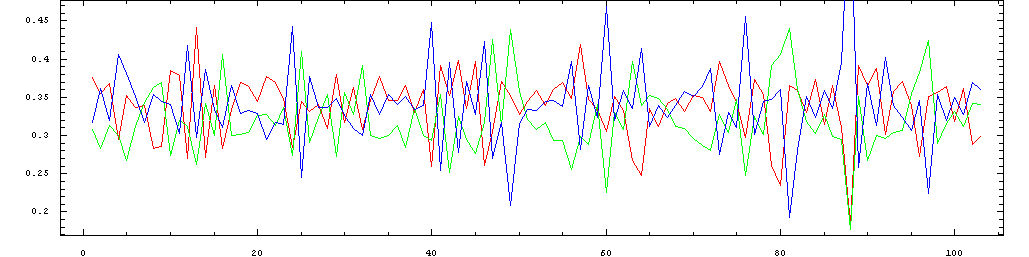
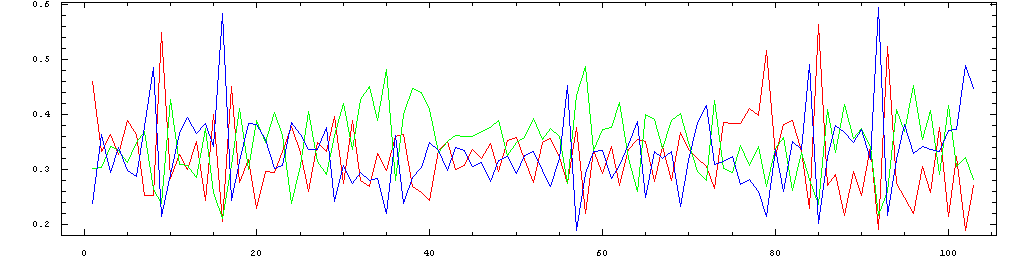
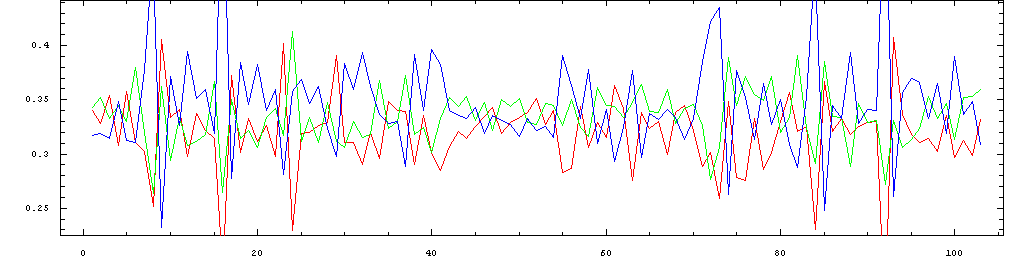
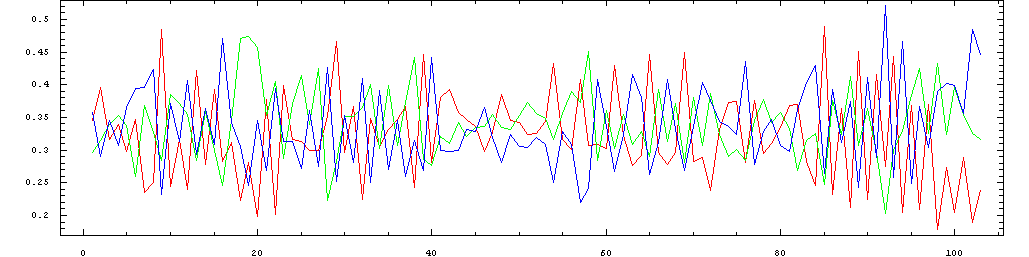
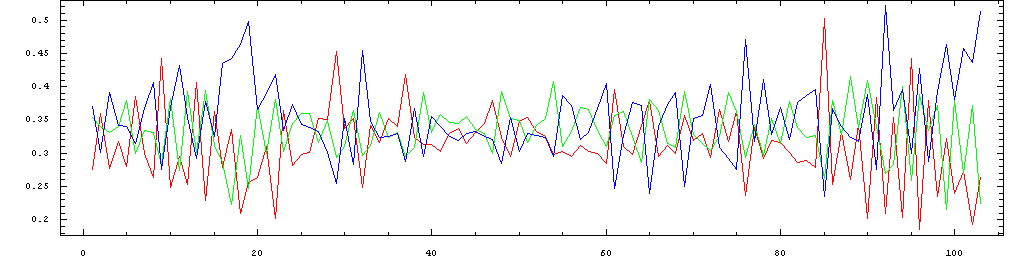
The following plots show the same data in sequence, so that the
pattern of metric stress of the individual beats can be seen as they
progress throughout the performance. The colors represent the same beats
in the metric cycle as in the plots above: red=1; green=2, blue=3.
Mazurka in A minor, Op. 7, No. 2 performed by Chiu in 1999:
Mazurka in A minor, Op. 7, No. 2 performed by Chiu in 1999 (raw tapping):
Mazurka in A minor, Op. 7, No. 2 performed by Friedman in 1930:
Mazurka in A minor, Op. 7, No. 2 performed by Friedman in 1930 (raw tapping):
Mazurka in F minor, Op. 7, No. 3 performed by Friedman in 1930:
Mazurka in F minor, Op. 7, No. 3 performed by Friedman in 1930 (raw tapping):
Mazurka in F minor, Op. 7, No. 3 performed by Rosen in 1989:
Mazurka in F minor, Op. 7, No. 3 performed by Rosen in 1989 (raw tapping):
Mathematica Notebook
Here is the Mathematica notebook used for calculations and
to generate the plots:
|



